El dueño de las pirámides
Parece mentira, pero no hay documental sobre el Antiguo Egipto que haya visto en los últimos dos años en el que este hombre no aparezca: me refiero al
Dr. Zahi Hawass, el director del Consejo Supremo de Antigüedades Egipcias.

Según
sus antecedentes académicos, Zahi Hawass es un arqueólogo reconocido y un erudito calificado en el tema, pero ¿por qué lo entrevistan en todos los documentales, como si fuera el galán de moda en gira de promoción? El tipo es simpático, ¿pero acaso no hay otro egiptólogo para entrevistar? ¿O es el único funcionario con autoridad para hablar sobre las antigüedades de su país?
De tanto verlo, casi me han hecho creer que es el dueño del lugar. Ya sea que se trate de excavaciones en la zona de las pirámides, del descubrimiento de alguna momia o de saqueadores de tumbas reales, el omnipresente Zahi Hawass siempre tiene algo que decir y algo que mostrar.
Por supuesto, no tengo nada en contra del doctor, pero me aburrió tanta exposición televisiva. Si siquiera sospecho que lo van a mostrar, cambio de canal: no más egiptología para mí por al menos un par de años.
Para quienes puedan soportar mayores dosis sin sobrecargarse,
aquí hay más información sobre el Dr. Zahi Hawass (
en inglés).
Aunque se me ocurre que habría sido más adecuado que la página estuviera escrita en jeroglíficos.Actualización: Buscando por la red
encontré muchos enlaces en castellano sobre Zahi Hawass, así que quienes no lo conozcan pueden formarse una opinión.
Calendario ficticio
Iván de
Juegos de ingenio preguntaba por un acontecimiento sucedido un 31 de junio que, por lo capcioso del asunto, supuse en primera instancia tenía el propósito de atrapar a los distraidos de siempre.
Sin embargo, buscando en Google por
31 de junio me vine a enterar que hay una buena cantidad de distraídos tropezando por el mundo, programando y proponiendo actividades que nunca podrán llevarse a cabo. Y si bien el 31 de junio es el más popular de los días oficialmente inexistentes, el culto del calendario ficticio se festeja también el
31 de abril, el
31 de septiembre —o
setiembre— y el
31 de noviembre.
¿Y febrero? Por el año bisiesto es el mes que más se presta a los equívocos y por esa razón creí que no era necesario agregarle más días. Poco imaginativo lo mío: hace mucho y en pocos países existió el
30 de febrero, de modo que no podría contarlo como un día absolutamente ficticio. Pero mi sorpresa fue total cuando buscando por
31 de febrero encontré pocos pero vigorosos indicios de un culto incipiente.
Pues parece entonces que el calendario ficticio llegó para quedarse, con sus días firmemente intercalados entre los días oficiales. Incluso no descarto un año futuro en el que los dìas ficticios sean más numerosos que los días reales. Es sólo cuestión de que los distraídos se esfuercen un poco más.
Conferencias y coloquios de Stephen Hawking
En
esta página pueden leerse o bajarse gratis, cinco conferencias públicas (
en inglés) del conocido físico y profesor
Stephen Hawking.
Habitual conferencista, muchas de las exposiciones públicas del profesor Hawking han sido compiladas en su libro
Agujeros Negros y Universos Bebés, y otros ensayos, publicado en 1993. Sin embargo las conferencias ofrecidas más arriba se llevaron a cabo en fecha reciente. Para facilitar la comprensión del tema se incluye un glosario de algunos de los términos usados.
En esta
otra página hay disponibles coloquios de física para leer o bajar gratis (
también en inglés). A diferencia de las conferencias públicas, los coloquios suponen un conocimiento avanzado de física.
Vía
Cynical C (
en inglés).
Nota: En
una de las conferencias,
Vida en el universo, Hawking trata un tópico muy cuestionado: el
principo antrópico. Defensor de la versión
débil del principio,
aquí hay una exposición del principio tomada de uno de los libros de Hawking. Reformulado, el principio antrópico sostiene que las leyes de las naturaleza son las que son porque posibilitan nuestra existencia, lo que supone un antropocentrismo no justificado. También algunos autores han derivado sustento teórico del principio antrópico para la doctrina del diseño inteligente, asunto que en mi opinión debilita aún más al principio.
En esta página se desarrollan los puntos mencionados y sus objeciones.
Hobbes - Leyes de naturaleza
Breve guía de los preceptos, reglas generales de la razón o leyes de naturaleza, extractados de los capítulos XIV y XV del
Leviatán, y enumeradas de una manera concisa, elemental y sin aclaraciones:
- Buscar la paz y seguirla, y autodefensa total: Que todo hombre debiera esforzarse por la paz, en la medida en que espere obtenerla, y que cuando no puede obtenerla, puede entonces buscar y usar toda la ayuda y las ventajas de la guerra, de cuya regla la primera fase contiene la primera y fundamental ley de naturaleza, que es buscar la paz, y seguirla, la segunda, la suma del derecho natural, que es defendernos por todos los medios que podamos.
- Renunciar al derecho natural en pro de la paz: Que un hombre esté dispuesto, cuando otros también lo están tanto como él, a renunciar a su derecho a toda cosa en pro de la paz y defensa propia que considere necesaria, y se contente con tanta libertad frente a otros hombres como consentiría a otros hombres frente a él mismo.
- La justicia: Que los hombres cumplan los pactos que han celebrado.
- La gratitud: Que un hombre que reciba beneficio de otro por mera gracia se esfuerce para que aquel que lo haya dado no tenga causa razonable para arrepentirse de su buena voluntad.
- La complacencia o deferencia: Que todo hombre se esfuerce por acomodarse al resto de los hombres.
- El perdón: Que ante garantía para el tiempo futuro, un hombre debiera perdonar las ofensas pasadas de aquellos que, arrepentidos, lo desean.
- Misericordia: Que en las venganzas (esto es, en la retribución de mal por mal) los hombres no miren la magnitud del mal pasado, sino la magnitud del bien por venir.
- Contumelia o insolencia: Que ningún hombre declare odio o desprecio de otro por obra, palabra, aspecto, o gesto.
- Contra el orgullo: Que todo hombre reconozca a los demás como sus iguales por naturaleza.
- Modestia o contra la arrogancia: Que al iniciarse las condiciones de paz, ningún hombre requiera reservar para sí mismo derecho alguno que no esté dispuesto sea reservado para cada uno de los demás.
- Equidad: Si se confía en un hombre para que juzgue entre hombre y hombre, es precepto de la ley de naturaleza que medie con igualdad entre ellos.
- Uso igual de cosas comunes: Que las cosas que no son divisibles sean gozadas si puede ser en común y, si lo permite la cantidad de la cosa, sin reserva; en otro caso, proporcionalmente al número de aquellos que tienen derecho.
- De la suerte: Que el derecho entero o (alternativamente) la primera posesión, sea determinada por suerte.
- De la progenitura y del primer establecimiento: Que aquellas cosas que no pueden ser gozadas en común ni divididas, sean adjudicadas al primer poseedor y, en algunos casos, al primer nacido, como adquiridas por suerte.
- De los mediadores: Que se le otorgue salvoconducto a todo hombre que medie por la paz.
- Sumisión al arbitraje: Que aquellos que están en controversia sometan su derecho al juicio de un árbitro.
- Nadie es juez de si propio: Ningún hombre es un árbitro adecuado para su propia causa.
- Nadie puede ser juez cuando tiene una causa natural de parcialidad: En ninguna causa debiera recibirse como árbitro a un hombre para el que pudiera aparentemente derivarse mayor beneficio, honor o placer, de la victoria de una parte que de la de otra.
- De los testigos: Y no pudiendo el juez en una controversia de hecho confiar más en uno que en otro (si no hay otros argumentos), deberá confiar en un tercero, o en un tercero y un cuarto, o en más.
Novedades del Mac en castellano
Para mantenerte al día con las novedades del mundo Mac y en castellano, reaparece una vez más
MacNoticias, renovado, en formato blog y con canal RSS.
También envían un
boletín de novedades por correo electrónico, al que pueden suscribirse en el blog.
Espero que esta nueva etapa dure bastante. A veces desaparecen de improviso y tan inexplicablemente como cuando vuelven a publicar. Para evitar el síndrome de abstinencia, aquí hay otros servicios de noticias —elijan ustedes cuál les gusta más—:
Midgley sobre Wittgenstein
Mary Midgley —una filósofa británica especializada en ética, que se hizo conocida en los ochenta por polemizar con
Richard Dawkins sobre su teoría del
gen egoísta— cuenta en
este reportaje (
en inglés) que al regresar a Oxford al término de la Segunda Guerra Mundial, tuvo la oportunidad de asistir a una conferencia de
Ludwig Wittgenstein:
No pude obtener casi nada de la conferencia, dice riendo. Wittgenstein era un hombre terriblemente tímido y se dirigía a la audiencia de un modo vacilante e impenetrable, de manera que era casi tan difícil entenderlo en persona como en sus escritos. Supongo que sus alumnos de Cambridge se habían acostumbrado a ese estilo, pero yo no pude. Sin embargo, Wittgenstein tenía un carisma indudable: era imposible no advertir que se estaba en presencia de una fuerza natural. Y fue una fuerza que se mantuvo por muchos años. Fue por medio del enfoque wittgensteiniano en el lenguaje que comenzamos a romper la soledad cartesiana del cogito ergo sum.
Nota: El programa de esta semana del ciclo
Grandes Filósofos está dedicado a Wittgenstein.
Entrada relacionada.
Sobre la correspondencia entre Martin Heidegger y Hannah Arendt
Aquí pueden leer el artículo que
George Steiner publicó sobre la edición de la correspondencia de
Martin Heidegger y
Hannah Arendt —publicado en The Times Literary Supplement el 29 de enero de 1999 y luego en la Revista de Occidente Nro. 220. Ante la falta del libro —creo que está publicado por Herder—, bien vale una reseña.
¿Por qué interesarnos en esta correspondencia? Como destaca Steiner, la celebridad de ambos protagonistas y las circunstancias políticas y filosóficas, convierten a esta relación en un caso muy especial —y
frágil, ante el chismorreo y la avidez de novedades del negocio periodístico. Por otro lado, el interés de la correspondencia excede al del drama privado que reflejan.
La relación entre ambos filósofos —que se conservó, con interrupciones, de por vida— comienza ochenta años atrás:
El primer encuentro entre ambos en noviembre de 1924, en el seminario de Heidegger en Marburg, se ha convertido en un acontecimiento legendario. Arendt había llegado de Königsberg, la ciudad de Kant, para estudiar con un profesor al que, ya en época tan temprana, los rumores que circulaban por todos los ambientes académicos de Alemania calificaban de "rey secreto del pensamiento" (lo que supondría la coronación de la propia Arendt). El chic sensual de Hannah contrastaba llamativamente con la grisura del ambiente estudiantil en el austero provincianismo del Marburgo posterior a 1918. La calculada rusticidad de Heidegger, su hipnótico sistema de enseñanza, aquellos famosos silencios que reducían a los alumnos más inteligentes a un fascinado terror, hechizaron a Fräulein Arendt. Si podemos fiarnos de lo que nos cuentan los testigos, fue ella la que solicitó a Herr Professor -una jugada audaz que evidentemente hizo que él se sintiera halagado y excitado-. Parece ser que fue en febrero de 1925 cuando se llegó a "lo concreto", por decirlo con la deliciosa expresión que utiliza Ursula Ludz.
Además, la relación amorosa se inscribe en una relación filosófica más amplia, triangular: entre el egoísmo de Heidegger y el atormentado papel de Arendt, tercia
Karl Jaspers, a modo de caballero al rescate. Como suele ocurrir en las publicaciones de los últimos veinticinco años, es Heidegger quien recibe la mayor parte de los palos privados; en la cuestión filosófica pocos se atreven a tanto.
Continúa.
FontExplorer X gratis
En estos días
LinoType habilitó la
descarga gratuita de la versión completa de
FontExplorer X (4,9 MB), un nuevo programa para la gestión de tipografías —o tipos de letra, como las llama Apple.

Según la empresa desarrolladora, la aplicación viene a llenar un vacío en la gestión de tipografías del
Mac OS X y la anuncia como una herramienta potente y fácil de usar, provista con todas las funciones que un usuario exigente —léase un diseñador gráfico— necesita: instalación personalizada, gestión avanzada de tipografías —activación y desactivación de tipos de letras y colecciones, vaciado de caches, compatibilidad con las colecciones tipográficas de Apple—, información sobre las características de un tipo de letra, previsualización personalizable y detallada por familias y por caracteres, integración con Mac OS X —es compatible con Spotlight y funciona con Mac OS X 10.3.9 o posterior—, activación automática de tipografías en todo el sistema y, en particular, compatibilidad con Adobe InDesign Support y Quark XPress Support.
En resumen, una maravilla, según lo anunciado. Ahora bien, cualquier usuario con un poco de experiencia ya sabe que no es oro todo lo que reluce: ¿hay alguien interesado en probar esta aplicación? ¿Experiencias, comentarios? Yo sigo en el Mac OS X 10.3.8, sin tiempo para actualizarme.
También hay para bajar una versión anterior para
Windows —98/NT/2000 o posterior— y
Mac OS —8.6 y 9.x—. Los enlaces para descargar las aplicaciones están a la derecha de la página.
Libros de George Orwell online
Una gran colección de las principales obras de George Orwell (
en inglés y
en ruso), de acceso libre y gratuito.

La biblioteca se divide en seis grandes categorías: novelas, ensayos, artículos, reseñas, poemas y artículos sobre el escritor. Entre sus novelas, hay enlaces para leer online o bajar:
- Down and Out in Paris and London
- Burmese Days
- A Clergyman's Daughter
- Keep the Aspidistra Flying
- The Road to Wigan Pier
- Homage to Catalonia
- Coming up for Air
- Animal Farm: A Fairy Story
- Nineteen Eighty-Four
La página también ofrece una selección de ciento cincuenta
fotografías acerca de la vida de Orwell (la ilustración que acompaña la entrada es de
Alex Hughes), extractos de
George Orwell: A Life, una biografía escrita por
Sir Bernard Crick y
artículos sobre aspectos fundamentales de la obra del escritor, así como de su relevancia actual.
Entrada relacionada:
Orwell, lenguaje y gobierno totalitario.
Vía
Boing Boing (
en inglés).
Una roca no lejos de Surlei

Desde que leí por primera vez el
Ecce homo me preguntaba acerca de esa roca, quizás un aspecto trivial de la cuestión del
eterno retorno, pero también en cierto modo una manera de reconstruir —a la distancia y siempre en ella— la magia única del acontecer súbito de un pensamiento central de la filosofía de Nietzsche, pues Zaratustra es el maestro del eterno retorno.
Este es el texto al que me refiero:
Voy a contar ahora la historia del Zaratustra. La concepción fundamental de la obra, el pensamiento del eterno retorno, esa fórmula suprema de afirmación a que se puede llegar en absoluto, — es de agosto del año 1881: se encuentra anotado en una hoja a cuyo final está escrito: "A 6.000 pies más allá del hombre y del tiempo". Aquel día caminaba yo junto al lago de Silvaplana a través de los bosques; junto a una imponente roca que se eleva en forma de pirámide no lejos de Surlei, me detuve. Entonces me vino ese pensamiento. — Si me remonto algunos meses hacia atrás a partir de aquel día, encuentro, como signo precursor, un cambio súbito y, en lo más hondo, decisivo de mi gusto, sobre todo en la música. Acaso sea lícito considerar el Zaratustra entero como música; — ciertamente una de sus condiciones previas fue un renacimiento en el arte de oír.
Tomado de Friedrich Nietzsche,
Ecce homo, del capítulo dedicado a
Así habló Zaratustra, Un libro para todos y para nadie, Ed. Alianza, pág. 93.
Texto completo de la hoja mencionada por Nietzsche en el párrafo citado.
La imagen fue tomada de
esta página (se necesita de
Flash Player 6 para visualizarla correctamente). En esta
otra página hay una película de 360° en
QTVR —de sólo 505 KB— de la habitación que Nietzsche ocupó en Sils-María durante los veranos de 1881 y de 1883 a 1888, y donde escribió la segunda parte del
Zaratustra,
Más allá del bien y del mal,
La genealogía de la moral,
El crepúsculo de los ídolos y
El anticristo.
Nota:
QTVR o
QuickTime Virtual Reality, es una tecnología multiplataforma desarrollada por
Apple que permite recorrer un espacio virtual de una manera muy similar a como se percibe la realidad. Una película QTVR permite que el observador interactúe hasta cierto punto con la imagen, pudiéndose mover hacia uno u otro lado, hacia arriba o hacia abajo (
mantener apretado el botón del ratón mientras se lo desplaza en la dirección deseada), realizar acercamientos (
pulsar la tecla mayúscula) o alejamientos (
pulsar la tecla control).
Killer Su Doku online
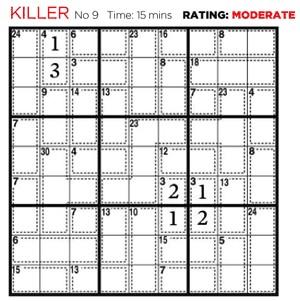
Una vez presentado el
Killer Su Doku, y mostrado un
ejemplo deductivo de resolución, quienes quieran seguir jugando habrán notado la sequía: no es fácil encontrar más juegos para resolver online.
La buena noticia es que
The Times publica todos los días un
killer, además de dos
Sudoku (o
Sudokus) tradicionales. La mala es que la versión online del día no los incluye —yo, al menos, no los pude encontrar.
La única manera de acceder a los juegos es por medio del buscador de la página, ubicado en la parte superior izquierda. Se busca por
su doku, en la ventanita que se abre se acepta en el recuadro que dice
Search the site o
Buscar en la página —para los lectores no suscriptos al medio, el sistema sólo permite buscar en los últimos siete días— y luego se hace clic en un enlace como este:
Su Doku: September 12, 2005.
Nota: Es decepcionante que además de las sumas hayan agregado al
killer algunos números iniciales, me parece que el juego es ahora mucho más fácil de resolver —este
asesino perdona.
Itokawa
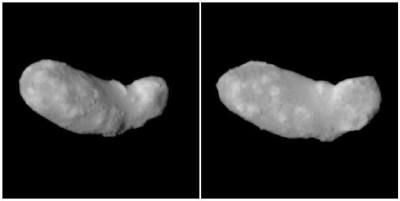
Imágenes del asteroide
Itokawa (1998 SF36) tomadas por la sonda japonesa
Hayabusa desde unos 20 kilómetros.
La misión de la Hayabusa —lanzada en mayo de 2003— es descender autónomamente en el asteroide —los casi diez minutos de retraso en las comunicaciones hacen imposible el control desde la Tierra—, recolectar muestras y traerlas de regreso a la Tierra.
Si la misión es exitosa, en junio de 2007 las muestras descenderán a la superficie de nuestro planeta en paracaídas y la Hayabusa será la primera misión espacial en haberlo conseguido.
Más información en
Space.com (
en inglés).
Nota: Si no te habías enterado de esta misión es porque para los medios tradicionales las misiones espaciales no son importantes en sí mismas sino
quién las lleva a cabo.
Actualización: Nuevas imágenes tomadas por la sonda
Hayabusa del
Itokawa a medida que el asteroide rotaba sobre su eje.
Imagen color del asteroide, creada por la combinación de tres imágenes individuales tomadas con un filtro rojo, uno verde y otro azul.
Mezclando los tantos
Como a veces me preguntan por ejemplos de sofismas, aquí va uno:
el blog el sofista es más importante que el diálogo platónico El sofista o del Ser porque está mejor ubicado en Google.
Nuevo mapa color de Plutón
Basándose en imágenes tomadas por el
Telescopio Espacial Hubble entre julio de 2002 y junio de 2003, astrónomos del Observatorio Lowell realizaron un nuevo mapa color de
Plutón. Con la información capturada durante doce órbitas del telescopio y la aplicación de dos filtros, la imagen llevó más de dos años de proceso informático para generarse.
 Ver imagen más grande
Ver imagen más grande, con coordenadas.
Según los astrónomos, en el mapa se observan áreas oscuras que se cree serían de hielo de agua sucio y áreas más brillantes que indican la presencia de nitrógeno congelado. Las áreas rojizas podrían deberse a hielo de metano y posiblemente de otros compuestos orgánicos, como las moléculas basadas en el carbono.
El metano congelado parece abarcar toda la superficie del planeta, mientras que el punto brillante cercano al centro del mapa podría indicar la presencia de monóxido de carbono. Habrá que esperar hasta el 2015, cuando llegue la sonda
Nuevos Horizontes o
New Horizons a Plutón para develar el misterio.
Por otro lado, un equipo del Observatorio de París pudo establecer el diámetro y la densidad de
Caronte, la luna de Plutón, con mayor precisión, utilizando las observaciones realizadas durante la ocultación de la luna el 11 de julio de este año. Según estas estimaciones, el radio de Caronte es de 602,5 km —el margen de error es de un kilómetro en más o en menos—, y la densidad es de 1,73 gramos por centímetro cúbico, siendo 0,08 el margen de error.
Y todo eso sin siquiera mencionar la polémica sobre el estatus planetario de Plutón.
Más información (
en inglés).
Nota: La imagen no está corrupta ni fuera de foco; aunque un poco decepcionante e indescifrable para los legos como nosotros, para los astrónomos es todo un hito.
Fractales
Una
excelente galería de
fractales. Típicamente realizados por computadora, el fractal es una conocida clase de objetos geométricos que no varían cuando se cambia la escala de presentación.

Como las imágenes son muy numerosas y de diferente tipo,
Jos Leys —el autor de la página y del
arte fractal— clasificó a los fractales en cuatro grandes categorías —geométricos, monstruos y criaturas extrañas (
en la imagen), objetos de Klein y animaciones—, cada una de las cuales está dividida en numerosas subcategorías. Tanto es así que la exploración de la página lleva bastante tiempo y sin que uno se dé cuenta.
Algunas de las imágenes son muy hermosas, incluso
este fractal ganó el premio al mejor de la exposición en la edición del 2002 del concurso organizado por el
Museo de Arte Informático (MOCA).
Vía
The Presurfer (
en inglés).
Ciclo Grandes Filósofos
Teniéndole poca simpatía a la televisión, pocas veces recomiendo un programa, pero éste sale de la mediocridad general. Me refiero al ciclo
Grandes Filósofos, que se emite por
Canal (á), de Argentina, los miércoles a las 00:00, 3:30, 7:30, 13:30, 17:30, 20:30 hs, los sábados a las 16:00 hs. y los domingos a las 7.30 hs.
Tal como señala la presentación oficial del ciclo:
El ciclo recorrerá la vida y obra de los grandes filósofos desde sus orígenes en la Antigua Grecia hasta la actualidad. Estos hombres marcaron el rumbo del pensamiento actual. El ciclo de 26 capítulos contará con entrevistas a especialistas en cada temática y cada autor. Algunos de los filósofos con que contará la serie son Aristóteles, Immanuel Kant, [Georg] Hegel, Karl Marx, Friedrich Nietzsche, Michel Foucault, entre muchos otros.
Hasta ahora vi los capitulos dedicados a Hegel, Kierkegaard, Schopenhauer, Nietzsche y Russell. La mayoría de los entrevistados —tres o cuatro por capítulo— son docentes de la Universidad de Buenos Aires y, si bien el nivel es accesible y puede servir como introducción a cada uno de los filósofos, lo aprovecharán mejor quienes tengan un cierto conocimiento de la especialidad.
Los próximos programas estarán dedicados a Edmund Husserl, Martín Heidegger, Jean Paul Sartre y Michel Foucault.
Partida desde la Tierra
El 2 de agosto pasado, la sonda espacial
Messenger de la NASA tomó cientos de fotografías de la Tierra, cuando utilizando el empuje de la gravedad de nuestro planeta cambió de trayectoria para impulsarse hacia su próximo destino, el planeta Venus.

Con la secuencia de fotografías se creó una película a fin de documentar la vista de la Tierra desde la Messenger a medida que ésta se alejaba de la Tierra. La película está compuesta por 358 cuadros fotografiados a lo largo de 24 horas y muestra una rotación completa de la Tierra sobre su eje. Cuando el 2 de agosto comenzó a fotografiar a la Tierra, la sonda estaba a unos 65 mil kilómetros por encima de América del Sur y, al momento de la última fotografía, tomada un día después, ya se había alejado unos 435 mil kilómetros del planeta e, incluso, más allá de la órbita de la Luna.
La película puede verse con cualquier navegador que tenga instalado
QuickTime o descargarse libre y gratuitamente en dos versiones:
rotación de la Tierra (4,90 MB) o
rotación de la Tierra con fecha y hora (5,78 MB).
Reloj binario
Lo usaba hace unos dos años como salvapantallas, pero lo perdí en la actualización al Mac OS X 10.3 (Panther). En
esta página (
en inglés) explican cómo funciona:
Como en cualquier reloj digital, se lee de izquierda a derecha. Así las dos primeras columnas representan la hora, las dos columnas del medio los minutos y las últimas dos los segundos. Además, cada fila representa las potencias de dos, de abajo arriba; 1, 2, 4 y 8. Para averiguar la hora, sólo hay que sumar los valores asociados a cada cuadrado activo (
en naranja) de cada columna. Si no hay cuadrados activos en una columna, el valor es 0.

Por ejemplo, la imagen muestra que sólo la posición 4 está activa en la segunda columna contando desde la derecha, por lo tanto los segundos estarán en el orden de las cuatro decenas. A su derecha, las posiciones 4 y 1 están activas, para un total de 5. Así, yuxtaponiendo ambos números, averiguamos que los segundos de la medida de la hora son 45. Sumando las columnas restantes, averiguamos que la hora es 22:47:45.
Al principio no resulta fácil —en particular porque las columnas de los segundos se actualizan muy rápido
obviamente—, de modo que lo mejor es practicar con las columnas de los minutos y de las decenas de segundos.
Aplicando el mismo truco se puede
contar hasta 31 con los dedos de una mano (para ver el ejemplo se necesita
Flash Player 6). Y para los muy fanáticos, combinando los dedos de ambas manos, hasta 1023. Y no sigo porque ahora no me puedo descalzar.
Darse cuenta
Como ven,
perder el tiempo me lleva mucho tiempo.
Ejemplo deductivo de Killer Su Doku
A modo de ejemplo y por demanda popular, detallo cómo deduje el ejemplo de
Killer Su Doku mencionado ayer (
en la imagen). Como suele ocurrir en estos casos, es mucho más simple resolver el puzzle que explicar el procedimiento —además la explicación es muy tediosa y es fácil perderse. Traté de explicitar todos los pasos realizados, pero no descarto que haya quedado alguno implícito.
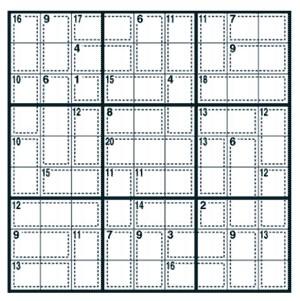
Para seguir la deducción es imprescindible que tengan a la vista la imagen del puzzle y vayan anotando los números. Como es habitual, las filas se numeran de arriba a abajo, las columnas de izquierda a derecha. Las coordenadas 1,3, por ejemplo, se leen fila 1, columna 3.
Las reglas que menciono son las básicas del
Sudoku original:
- Regla 1: Cada área se rellena con los números del 1 al 9, sin repetir ningún número.
- Regla 2: Cada fila se rellena con los números del 1 al 9, sin repetir ningún número.
- Regla 3: Cada columna se rellena con los números del 1 al 9, sin repetir ningún número.
Pasos:
- En 3,3 va 1.
- El grupo formado por 2,3 y 2,4, que suma 4, sólo puede ser suma de 3+1 (2+2 está excluído por regla 2; 1 no puede ir en 2,3 por regla 1). Por lo tanto, en 2,3 sólo puede ir 3 y 1 en 2,4.
- En 7,7 sólo puede ir 2.
- El grupo formado por 8,6 y 8,7, que suma 3, sólo puede ser suma de 2+1. 2 no puede ir en 8,7 por regla 1. Por lo tanto, 8,6 sólo puede ir 2 y 1 en 8,7.
- El grupo formado por 1,1 y 2,1, que suma 16, sólo puede ser suma de 9+7 (8+8 está excluído por regla 3).
- El grupo formado por 1,3 y 1,4, que suma 17, sólo puede ser suma de 9+8.
- Por 05, 06 y regla 2, 1,1 sólo puede ir 7 y 9 en 2,1.
- Por 06, 07 y regla 1, el 9 sólo puede ir en otra área, es decir, en 1,4. Por lo tanto, 1,3 sólo puede ir 8.
- El grupo formado por 3,6 y 4,6 sólo puede ser suma de 3+1 (2+2 está excluído por regla 3).
- Por 09, 02 y regla 1, el 1 sólo puede ir en otra área, es decir, en 4,6. Por lo tanto, en 3,6 sólo puede ir 3.
- El grupo formado por 3,2, 4,2 y 5,2, que suma 6, sólo puede ser suma de 1+2+3.
- Como la fila 3 y 4 ya tienen un 1, entonces por 11 y regla 2 sólo puede ir 1 en 5,2.
- Por 10, 11, 12 y regla 2, en 3,2 sólo puede ir 2 y 3 en 4,2.
- El grupo formado por 1,2 y 2,2, que suma 9, sólo puede ser suma de 4+5 (las sumas 8+1, 7+2 y 6+3 están excluídas por regla 1, pues al menos uno de los sumandos de cada uno de esos pares ya está puesto en el área).
- Por 14 y regla 1, sólo puede ir 6 en 3,1.
- El grupo formado por 3,1 y 4,1, que suma 10, por 15 sólo puede ser suma de 6+4. Por lo tanto, en 4,1 sólo puede ir 4.
- El grupo formado por 5,1 y 6,1, que suma 10, sólo puede ser suma de 8+2 (9+1 está excluído por regla 1; 7+3, 6+4 y 5+5 están excluídos por regla 3).
- El grupo formado por 6,2 y 6,3, que suma 15, sólo puede ser suma de 9+6 (8+7 está excluído por 17 y regla 1).
- El grupo formado por 4,3 y 5,3, que suma 12, sólo puede ser suma de 7+5 (por 17 y 18).
- El grupo formado por 5,8, 6,8 y 7,8, que suma 6, sólo puede ser suma de 1+2+3. Como 1 ya está en las filas 4 y 5, 1 sólo puede ir en 6,8.
- Por 03 y regla 1, en 5,8 sólo puede ir 2.
- Por 20 y 21, 7,8 sólo puede ir 3.
- Por 17, 21 y regla 2, en 5,1 sólo puede ir 8 y 2 en 6,1.
- El grupo formado por 1,5 y 2,5, que suma 6, sólo puede ser suma de 4+2 (5+1 está excluído por regla 1, porque 1 está en 2,4 por 02; 3+3 está excluído por regla 3).
- El grupo formado por 4,4 y 4,5, que suma 8, sólo puede ser suma de 6+2 (7+1 está excluído por 10 y regla 1 y 2; 4+4 está excluído por regla 2).
- Por 24, 25 y regla 3, 2 sólo puede ir 4,4. Por lo tanto, en 4,5 sólo puede ir 6.
- El grupo formado por 4,8 y 5,8, que suma 12, no puede ser suma de 6+6, por regla 3.
- El grupo formado por 5,7 y 6,7, que suma 13, sólo puede ser suma de 6+7; porque por 18, 6 ya está en la fila 6; por 26, 6 está en la fila 4; y por 27, 6 no puede ir 5,8.
- Por 28, en 5,7 sólo puede ir 6 y 7 en 6,7.
- En 4,3 sólo puede ir un 7, porque por 29 y regla 1, 7 no puede ir en 4,7, 4,8 y 4,9. Todos los otros lugares de la fila 4 fueron ocupados en pasos anteriores.
- Por 30 y 19, en 5,3 sólo puede ir 5.
- El grupo formado por 9,6 y 9,7, que suma 16, sólo puede ser suma de 9+7 (8+8 está excluído por regla 2).
- Por 29, 32 y regla 3, en 9,7 sólo puede ir 9.
- Por 32, en 9,6 sólo puede ir 7.
- El grupo formado por 6,5 y 6,6, que suma 11, sólo puede ser suma de 8+3 (9+2 y 6+5 están excluídos por 26 y regla 1; 7+4 está excluído por 29 y regla 2).
- Por 35, 10 y regla 3, en 6,5 sólo puede ir 3.
- Por 35 y 36, en 6,6 sólo puede ir 8.
- En 5,8 sólo puede ir un 3, porque por 36 y regla 2, ya hay un 3 en 6,5 y por 13 y regla 2, ya hay un 3 en 4,2. 5,7 y 5,8 fueron ocupados en pasos anteriores.
- Por 27 y 38, en 4,8 sólo puede haber un 9.
- El grupo formado por 4,7 y 4,8, que suma 13, sólo puede ser suma de 8+5 por regla 1.
- Por 40 y regla 1, en 6,9 sólo puede ir 4.
- El grupo formado por 6,9 y 7,9, que suma 12, por 41 sólo puede ser suma de 8+4.
- Por 41 y 42, en 7,9 sólo puede ir 8.
- El grupo formado por 8,9 y 9,9, que suma 13, sólo puede ser suma de 7+6 (9+4 y 8+5 están excluídos por regla 1).
- Por 44, 34 y regla 2, en 8,9 sólo puede ir 7.
- Por 44 y 45, en 9,9 sólo puede ir 6.
- El grupo formado por 8,8 y 9,8, que suma 9, sólo puede ser suma de 4+5 (8+1, 7+2 y 6+3 están excluídos por regla 1).
- Por 40, 47 y regla 3, en 4,7 sólo puede ir 5.
- Por 40 y 48, en 4,8 sólo puede ir 8.
- El grupo formado por 1,7 y 2,7, que suma 11, sólo puede ser suma de 8+3 (9+2, 7+4 y 6+5 están excluídos por regla 3).
- Por 08, 50 y regla 2, en 1,7 sólo puede ir 3.
- Por 50 y 51, en 2,7 sólo puede ir 8.
- Por regla 3, en 3,7 sólo puede ir 4.
- El grupo formado por 3,7, 3,8 y 3,9, que suma 18, sólo puede ser suma de 9+5+4 (por 53, en 3,7 hay un 4; 3,8 + 3,9 tienen que sumar 14; 8+6 está excluído por regla 1).
- Por 39, 54 y regla 3, en 3,9 sólo puede ir 5.
- Por 54 y 55, en 3,8 sólo puede ir 9.
- El grupo formado por 1,8 y 1,9, que suma 7, sólo puede ser suma de 6+1 (5+2 y 4+3 están excluídos por regla 1).
- Por 20, 57 y regla 3, en 1,8 sólo puede ir 6.
- Por 57 y 58, en 1,9 sólo puede ir 1.
- El grupo formado por 2,8 y 2,9, que suma 9, sólo puede ser suma de 7+2 (8+1, 6+3 y 4+5 están excluídos por regla 1).
- Por 45, 60 y regla 3, en 2,8 sólo puede ir 7.
- Por 60 y 61, en 2,9 sólo puede ir 2.
- Por 18 y regla 2, en 6,4 sólo puede ir 5.
- Por 63, el grupo formado por 6,4 y 7,4, que suma 11, sólo puede ser suma de 5+6.
- Por 64, en 7,4 sólo puede ir 6.
- Por 24, 61 y regla 2, en 2,5 sólo puede ir 4.
- Por 24 y 66, en 1,5 sólo puede ir 2.
- Por 14, 66 y regla 2, en 1,2 sólo puede ir 4.
- Por 14 y 67, en 2,2 sólo puede ir 5.
- El grupo formado por 1,6 y 2,6, que suma 11, sólo puede suma de 6+5 (9+2, 8+3 y 7+4 están excluídos por regla 1).
- Por 58, 71 y regla 2, en 1,6 sólo puede ir 5.
- Por 71 y 72, en 2,6 sólo puede ir 6.
- El grupo formado por 7,5 y 7,6, que suma 14, sólo puede ser suma de 9+5 (8+6 está excluído por regla 1 y 2).
- Por 72, 74 y regla 3, en 7,6 sólo puede ir 9.
- Por 74 y 75, en 7,5 sólo puede ir 5.
- Por reglas 1 y 2, el grupo formado por 5,4, 5,5 y 5,6, que suma 20, sólo pued ser suma de 9+7+4.
- Por 77, 08, 75 y regla 3, en 5,5 sólo puede ir 9.
- Por 77, 78, 34 y regla 3, en 5,4 sólo puede ir 7.
- Por regla 1, en 5,6 sólo puede ir 4.
- El grupo formado por 3,4 y 3,5, que suma 15, sólo puede ser suma de 8+7 (9+6 está excluído por regla 1).
- Por 81, 79 y regla 3, en 3,4 sólo puede ir 8.
- Por 81 y 82, en 3,5 sólo puede ir 7.
- Por regla 3, el grupo formado por 8,5 y 9,5, que suma 9, sólo puede ser suma de 8+1.
- Por 84, 04 y regla 2, en 8,5 sólo puede ir 8.
- Por 84 y 85, en 9,5 sólo puede ir 1.
- Por regla 2, el grupo formado por 7,1, 7,2 y 7,3, que suma 12, sólo puede ser suma de 7+4+1.
- Por 07, 30, 87 y regla 3, en 7,2 sólo puede ir 7.
- Por 01, 87, 88 y regla 3, en 7,1 sólo puede ir 1.
- Por regla 2, en 7,3 sólo puede ir 4.
- Por regla 3, el grupo formado por 8,3 y 9,3, que suma 11, sólo puede ser suma de 9+2.
- Por 91, 04 y regla 2, en 8,3 sólo puede ir 9.
- Por 91 y 92, en 9,3 sólo puede ir 2.
- Por 92, 18 y regla 3, en 6,3 sólo puede ir 6.
- Por regla 3, en 6,2 sólo puede ir 9.
- Por regla 1, el grupo formado por 8,1 y 8,2, que suma 9, sólo puede ser suma de 6+3.
- Por 96, 15 y regla 3, en 8,1 sólo puede ir 3.
- Por 96 y 97, en 8,2 sólo puede ir 6.
- Por regla 1, el grupo formado por 9,1 y 9,2, que suma 13, sólo puede ser suma de 8+5.
- Por 99, 23 y regla 3, en 9,1 sólo puede ir 5.
- Por regla 1, en 9,2 sólo puede ir 8.
- Por regla 1, el grupo formado por 8,4 y 9,4, que suma 7, sólo puede ser suma de 4+3.
- Por 97, 102 y regla 2, en 8,4 sólo puede ir 4.
- Por regla 1, en 9,4 sólo puede ir 3.
- Por 47, 103 y regla 2, en 8,8 sólo puede ir 5.
- Por regla 1, en 9,8 sólo puede ir 4.
Listo. La máquina deductiva
ist Kaput. Avisen cualquier error.
Killer Su Doku
Una variante del puzzle lógico
Sudoku (o
Su Doku), que el diario londinense
The Times llama
Killer Su Doku.
El objetivo del
Sudoku original es rellenar un cuadrado de 9x9 dividido en nueve áreas de 3x3 con números, de forma tal que cada fila, cada columna y cada una de las nueve áreas contenga los números del 1 al 9. En la nueva forma del juego se respetan estas reglas, pero en vez de colocarse algunos números iniciales a partir de los cuales se deducen los restantes, se agrupan algunas casillas por medio de una línea punteada y se da la suma de los números agrupados.
Ejemplo.
Cuanto mayor es el grupo, mayor será el grado de dificultad del puzzle. Las versiones más fáciles del
Killer Su Doku tienen grupos de una sola casilla, lo que equivale a dar el número, como en la versión original del juego.
En la página del ejemplo se ofrecen cinco juegos de
Killer Su Doku con grados de dificultad creciente. El nivel inicial es realmente fácil, se resuelve en unos pocos minutos —si alguien quiere la solución, me la pide—; los niveles avanzados parecen difíciles, todavía no los intenté. Los diez primeros jugadores en enviar al periódico las cinco soluciones correctas
tienen premio, aunque dudo que el concurso valga para todo el mundo.
Vía
HotLinks (
en inglés).
Actualización: Ejemplo de cómo deducir paso a paso un
Killer Su Doku.
Otra actualización: Cómo encontrar más
Killer Su Dokus para jugar online y gratis.
Cuentos cortos clásicos
Una
página con un centenar de cuentos cortos (
en inglés) de autores muy conocidos y de diversas nacionalidades.
El objetivo de
Classic Short Stories es que la gente redescubra a los cuentos cortos y la magia en la que nos envuelve su lectura, por cuanto percibieron —y está claro no son los únicos— que cada vez menos gente lee a estos clásicos. Así, la página publica cuentos de
Ambrose Bierce,
Anton Chekhov,
Charles Dickens,
D. H. Lawrence,
Edgar Allan Poe,
Gabriel Garcia Marquez,
George Orwell,
Guy de Maupassant,
H. G. Wells,
Herman Melville,
Honoré de Balzac,
Jack London,
James Joyce,
Mark Twain,
Nathaniel Hawthorne,
Prosper Mérimée,
Roald Dahl,
Rudyard Kipling,
Virginia Woolf y
Washington Irving, entre otros.
Como toda selección, la presente recopilación es necesariamente incompleta, aunque también es mejorable. Se siente, en particular, la ausencia de
Jorge Luis Borges.
La página también ofrece un
listado bibliográfico por autores, un
breve diccionario de términos antiguos mencionados en los cuentos publicados y una extensa sección de
enlaces a otras páginas de contenido similar.
Vía
Cynical-C (
en inglés).
Entrada relacionada:
Dos mil cuentos cortos clásicos.
Nueva Orleans bajo las aguas

Una
imagen satelital (3 MB, la imagen de arriba muestra sólo un sector) de la ciudad de
Nueva Orleans, luego del paso del huracán
Katrina. A consecuencias de la inundación, la casi totalidad de la ciudad se ha vuelto inhabitable y está siendo evacuada. Según las autoridades, pasarán meses antes de que todos los habitantes puedan volver a su vivienda —si es que vale la pena volver.
También comienzan a publicarse los primeras fotos del antes y el después de la inundación. Hay varios enlaces en esta
entrada de Boing Boing.
Actualización: Si uno va a
Google Maps y escribe
New Orleans en el campo de búsqueda, podrá ver que a la derecha de los botones
Map,
Satellite y
Hybrid se agregó el botón
Katrina.
 Según sus antecedentes académicos, Zahi Hawass es un arqueólogo reconocido y un erudito calificado en el tema, pero ¿por qué lo entrevistan en todos los documentales, como si fuera el galán de moda en gira de promoción? El tipo es simpático, ¿pero acaso no hay otro egiptólogo para entrevistar? ¿O es el único funcionario con autoridad para hablar sobre las antigüedades de su país?
Según sus antecedentes académicos, Zahi Hawass es un arqueólogo reconocido y un erudito calificado en el tema, pero ¿por qué lo entrevistan en todos los documentales, como si fuera el galán de moda en gira de promoción? El tipo es simpático, ¿pero acaso no hay otro egiptólogo para entrevistar? ¿O es el único funcionario con autoridad para hablar sobre las antigüedades de su país?











